DBSCAN From Scratch

This Jupyter Notebook provides a detailed, step-by-step guide on implementing the DBSCAN (Density-Based Spatial Clustering of Applications with Noise) clustering algorithm from scratch. It covers the following key areas:

• Sample data points

• Build \(\epsilon\)-neighbourhood

• Identify core, border, and noise points

• Assign clusters using Depth-First Search (DFS)

• Show clustering results

The clustering results depends the choice of \(\epsilon\) and \(minPts\).

import random
import numpy as np
from scipy.spatial.distance import pdist, squareform

import matplotlib as mpl
import matplotlib.pyplot as plt

cmap = plt.get_cmap('tab10')
colors = [cmap(i) for i in range(cmap.N)]

mpl.rcParams["font.size"] = 24
mpl.rcParams["lines.linewidth"] = 2

import networkx as nx

seed = 0
random.seed(seed)
np.random.seed(seed)
n_samples = 10
markersize = 100

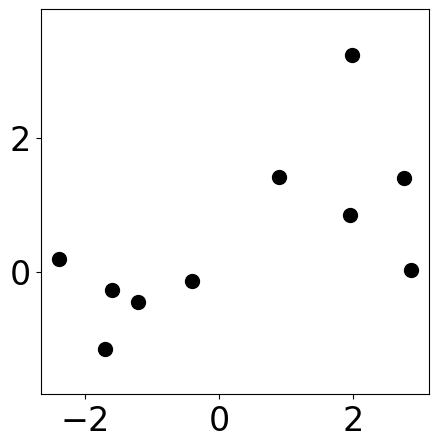
Sample data points

m1 = [1, 1]
cov1 = [[1, 0], [0, 1]]
s1 = np.random.multivariate_normal(m1, cov1, 5)

m2 = [-1, -1]
cov2 = [[1, -0.5], [-0.5, 1]]
s2 = np.random.multivariate_normal(m2, cov2, 5)

samples = np.concat([s1, s2])
np.random.shuffle(samples)

plt.figure(figsize=(5, 5))
plt.scatter(samples[:, 0], samples[:, 1], s=markersize, color="k")
plt.xlim([-2, 2])
plt.ylim([-2, 2])
plt.axis("equal")

(np.float64(-2.659691942232599),
 np.float64(3.1307603678824707),
 np.float64(-1.3757641112226862),
 np.float64(3.4607340235073694))

Build \(\epsilon\)-neighbourhood

eps = 2.0
# when min_samples=1,
# it is equivalent to find connected components
min_samples = 3

n_points = samples.shape[0]
distances = squareform(pdist(samples))

# create a networkx graph
G = nx.Graph()

# add nodes with positions
for i in range(n_points):
    G.add_node(i, pos=(samples[i, 0], samples[i, 1]))

# add edges according to distance cutoff
for i in range(n_points):
    for j in range(i + 1, n_points):
        if distances[i, j] < eps:
            G.add_edge(i, j)

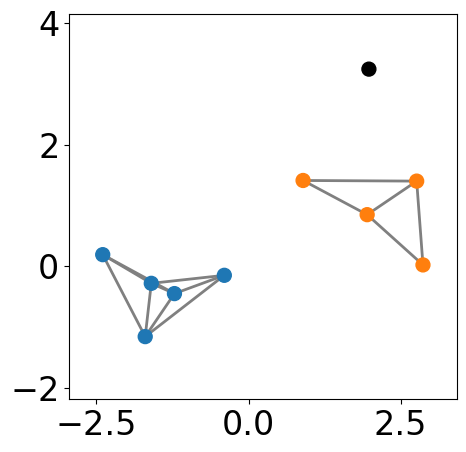
Identify core, border, and noise points

# find core points
core_points = []
for i in range(n_points):
    neighbors = list(G.neighbors(i))
    if len(neighbors) >= min_samples:
        core_points.append(i)

def core_border_noise(node):
    if node in core_points:
        return "core"
    else:
        neighbors = list(G.neighbors(node))
        connect_to_core = set(neighbors).intersection(core_points)
        if len(connect_to_core) >= 1:
            return "border"
        else:
            return "noise"

color_dct = {
    "core": "b",
    "border": "r",
    "noise": "k"
}

fig, ax = plt.subplots(figsize=(5, 5))
pos = nx.get_node_attributes(G, "pos")
nx.draw_networkx_nodes(G, pos,
        node_size=markersize, \
        node_color=[color_dct[core_border_noise(node)] for node in G], ax=ax)
nx.draw_networkx_edges(G, pos, edgelist=G.edges,
                       edge_color="gray", width=2)

ax.tick_params(left=True, bottom=True, labelleft=True, labelbottom=True)
plt.xlim([-2, 2])
plt.ylim([-2, 2])
plt.axis("equal")
plt.show()

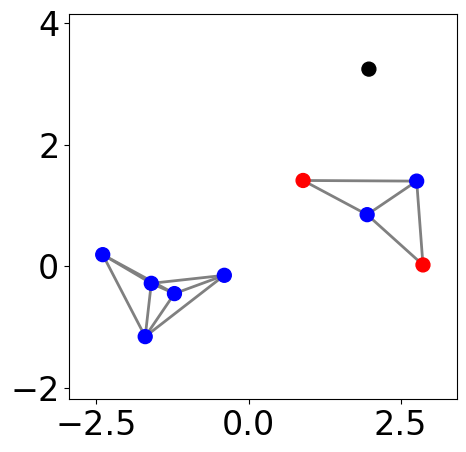
Assign clusters using Depth-First Search (DFS)

labels = np.full(n_points, -1)
cluster_id = 0

for core_point in core_points:
    if labels[core_point] == -1:
        stack = [core_point]
        # dfs-like search
        while stack:
            point = stack.pop()
            if labels[point] == -1:
                labels[point] = cluster_id
                neighbors = list(G.neighbors(point))
                for neighbor in neighbors:
                    if neighbor in core_points and labels[neighbor] == -1:
                        stack.append(neighbor)
                    else:
                        # truncate search for non-core point
                        labels[neighbor] = cluster_id
        cluster_id += 1

fig, ax = plt.subplots(figsize=(5, 5))
pos = nx.get_node_attributes(G, "pos")
nx.draw_networkx_nodes(G, pos,
        node_size=markersize, node_color=[colors[l] if l>=0 else "k" for l in labels], ax=ax)
nx.draw_networkx_edges(G, pos, edgelist=G.edges,
                       edge_color="gray", width=2)

ax.tick_params(left=True, bottom=True, labelleft=True, labelbottom=True)
plt.xlim([-2, 2])
plt.ylim([-2, 2])
plt.axis("equal")
plt.show()